In October 2024, we announced the winners of the LLM Zoomcamp 2024 Competition, where participants tackled high school math problems using large language models (LLMs). This challenge was part of our LLM Zoomcamp, a free course focused on real-world LLM applications.

In this article, we’ll share insights from the competition and spotlight some of the top solutions. Here’s what we’ll cover:
- Overview of the LLM Zoomcamp 2024 Competition
- Dataset Description
- Artur G’s Solution: Combining Code Generation with Chain-of-Thought Reasoning
- Blaqadonis’ Solution: Agent-based Approach Leveraging LangGraph
- Vladyslav Khaitov’s Hybrid Model Approach
- Slava Shen’s Solution: Blending Results with Data-Driven Logic
Overview of the LLM Zoomcamp 2024 Competition

The competition tasked participants with solving high school-level math problems from the Russian ЕГЭ exam using LLMs. The ЕГЭ exam is a standardized test required for admission to Russian universities and professional colleges.
We provided participants with the original problem statements in Russian and their English translations, generated by GPT-4. The goal was to solve these problems using LLMs without manual intervention.
Dataset Description
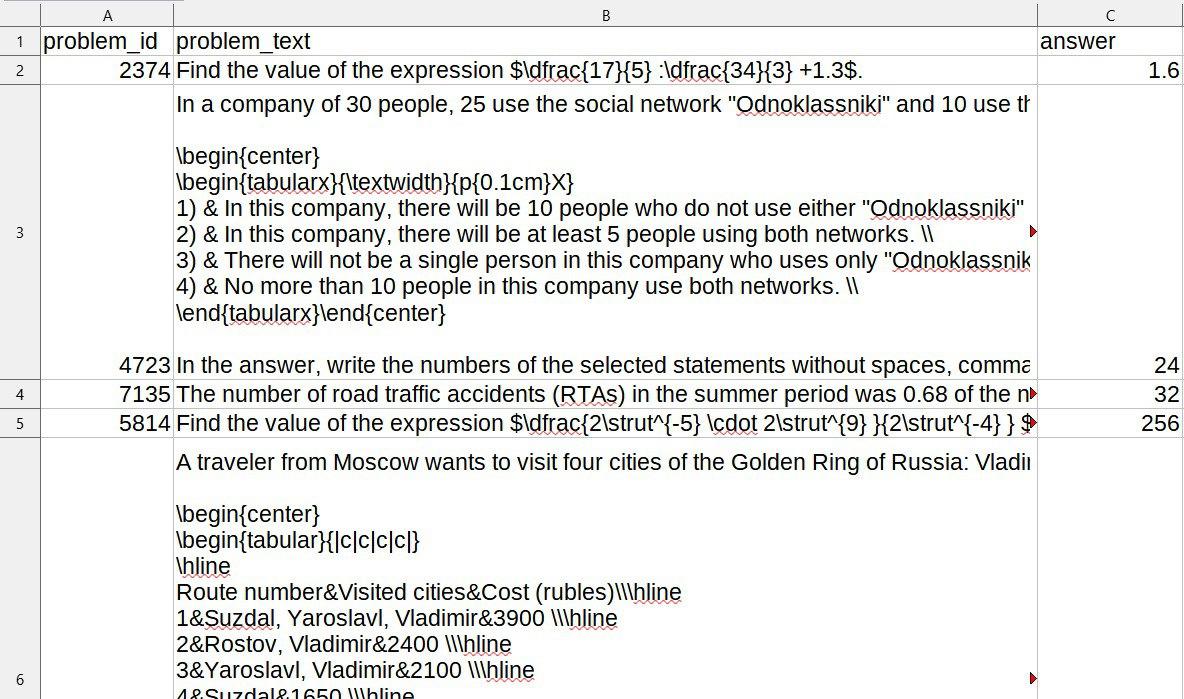
The dataset for the competition consisted of several CSV files containing training and test data. Key components of the dataset included:
- Training Data: Contained problem statements in English and Russian, answers, and hints. The data also included unchecked entries that might contain errors.
- Test Data: Required participants to predict the correct answers based on the problem statements in both languages.
- Sample Submission File: Offered guidance on the expected format for final submissions.
Now, let’s take a closer look at the winning solutions and the approaches behind them.
Artur G’s Solution: Combining Code Generation with Chain-of-Thought Reasoning
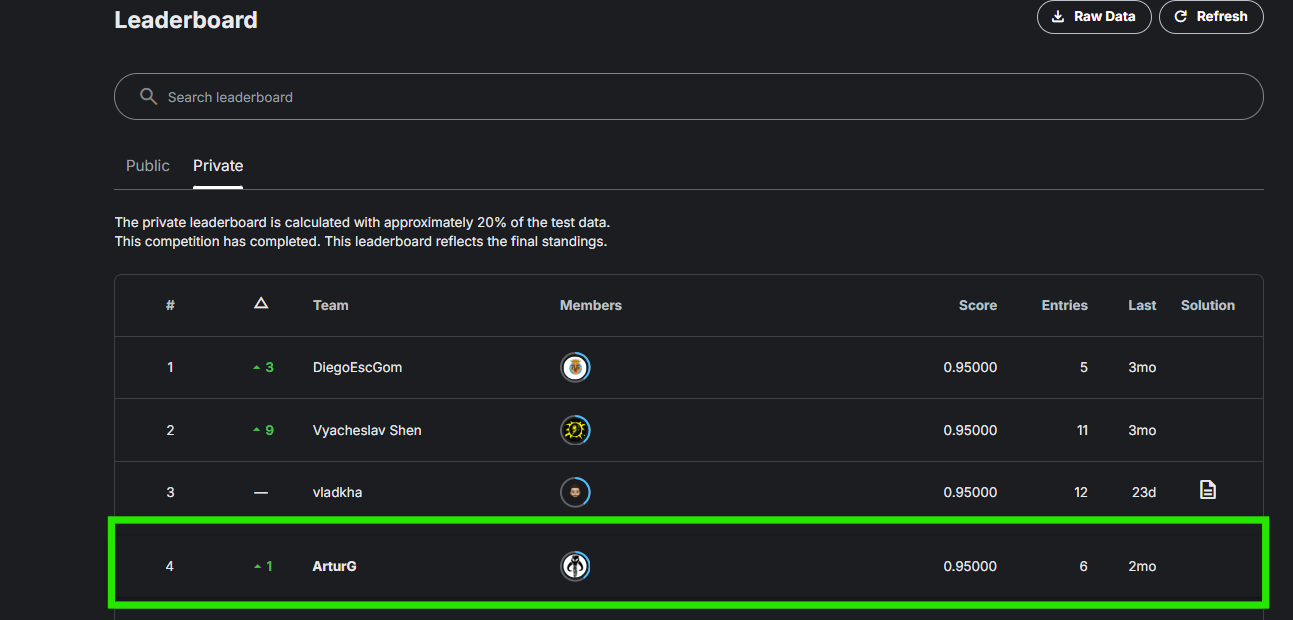
Artur G’s solution used Claude-3.5 Sonnet’s natural language understanding and Python code generation capabilities. He applied the Zero-shot Chain-of-Thought technique to prompt Claude-3.5 Sonnet to reason through problems and created two solutions:
- Solution 1: Reasoning without code.
- Solution 2: Reasoning supported by Python code execution.
To select the final solution, Artur compared the results from both approaches. If they matched, the answer was considered correct. If they didn’t, an additional reasoning step was performed to refine the answer.
Artur’s solution also included several safeguards:
- Instructor validation to ensure the Python code was executable.
- A timeout mechanism to prevent infinite loops.
- Error handling that allowed for retries in case of code failures.
Here are Artur’s key takeaway from this competition:
One might wonder if LLMs are useful to solve math problems. My answer is yes; the techniques I used, such as structured outputs, chain of thought reasoning, multithreading, and error handling with retry mechanisms, can elevate most LLM-based applications to the next level.
Blaqadonis’ Solution: Agent-based Approach Leveraging LangGraph
Blaqadonis’s solution used an agent-based approach, coordinating two models: OpenAI’s GPT-4 Omni and Meta’s Llama 3.1 70B through LangGraph, a low-level framework for building stateful AI applications. His solution achieved high accuracy at a cost of less than $3 per test run.
Blaqadonis used the Groq API to handle rate limits and avoid throttling. With a leaderboard score of 96.25%, his solution showcased the scalability and cost-effectiveness of agentic systems in solving complex problems. He also noted some challenges in the reliability of such systems.
Reflecting on his experience, Blaqadonis said:
What impressed me most was the leap in reasoning capabilities from GPT-3.5 Turbo to the current models. This improvement was reflected in the leaderboard scores: from 90% to 96.25% using agents. Among the latest models, there was a significant gap between the GPT-4o-mini and the original GPT-4o.
Vladyslav Khaitov’s Hybrid Model Approach

Vladyslav Khaitov’s solution combined open-source NuminaMath-7B-TIR-GPTQ with GPT-4 Omni to balance cost and performance. His hybrid approach used different models for different tasks, achieving high accuracy and cost efficiency.
Vladyslav initially adapted a solution from the AI Mathematical Olympiad competition, which used the NuminaMath-7B-TIR-GPTQ math LLM and Python REPL. Then, for certain task types where this solution performed poorly, Vladyslav used OpenAI’s GPT-4o to handle those specific cases.
Key aspects of Vladyslav’s solution included:
- Majority voting: Running models multiple times and selecting the most common solution, a form of ensembling for LLMs. Vladyslav noted that while this required many runs, it significantly improved results.
- Extensive post-processing: Much of the post-processing came from the Numina solution, but Vladyslav added more to accommodate differences in data and task types.
- Prompt experimentation: Minimal prompts worked best for Numina, while structured prompts like “Please reason step by step, and put your final answer within
\\boxed{}” improved results for GPT-4o.
Vladyslav shared his conclusions from the competition:
Many open-source models (without tool use, like Mathstral) didn’t perform well enough. Even OpenAI GPT-4o-mini fell short. The difference between GPT-4o-mini and GPT-4o was significant.
Slava Shen’s Solution: Blending Results with Data-driven Logic
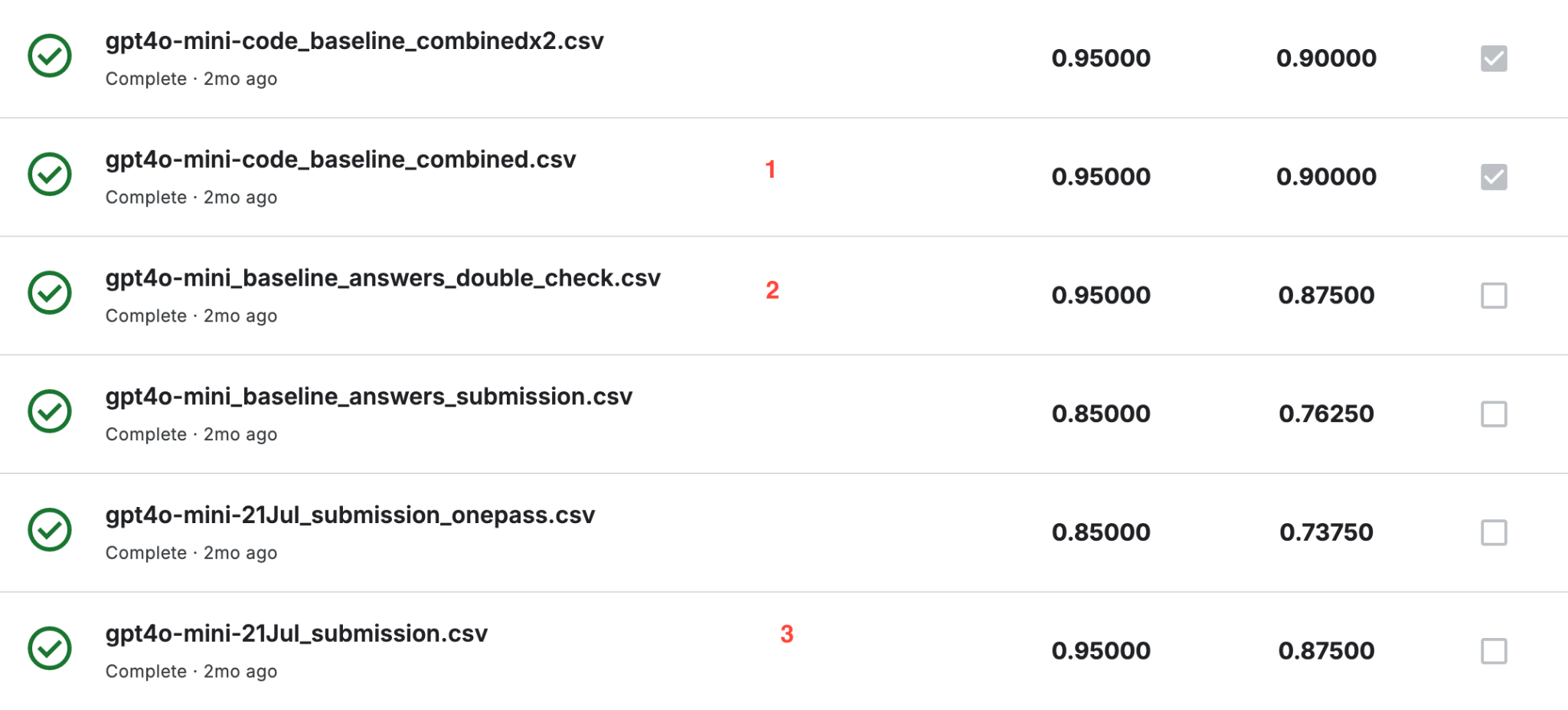
Slava Shen provided multiple solutions, all based on GPT-4o-mini:
- Solution 1: Combined solutions 2 and 3, with mismatches resolved through randomized selection based on a hyperparameter.
- Solution 2: A refined version of an initial Kaggle notebook with adjustments to prompts and temperature settings.
- Solution 3: The most complex approach, which involved dynamically constructing few-shot prompts using Elastic Search and running Python code extracted from the model’s output.
Slava’s solutions demonstrated flexibility and robustness, combining different models and methodologies, resulting in a final score of 95%.
Conclusion
The LLM Zoomcamp 2024 Competition was a great opportunity to test the limits of LLMs in solving structured mathematical problems. Participants explored diverse approaches, from blending open-source and closed-source models to using agentic systems and advanced prompt engineering techniques.